GET Solving the traveling salesman problem using the branch and bound method / Sudo Null IT News FREE

Hello, Habr! Implementing various algorithms for finding the least-cost Hamiltonian rhythm, I came across a publication offering its own version. After trying in practice, I got the wrong response:

Further searches on the Internet did non bring the hoped-for leave: either a complicated theoretical description for not-mathematicians, or an understandable one, but with errors.

Low the bring down you will represent waiting for the corrected algorithmic rule and online calculator.

The method itself, published away Little, Merty, Sweeney, Carel in 1963, is applicable to many NP-complete problems, and is a same theorized material, which without good knowledge of English language and mathematics cannot be immediately applied to our traveling salesman job.

Briefly about the method acting - this is a complete enumeration of wholly possible options with a screening of distinctly non-best solutions.

Rectified algorithm to find a truly minimal route

The algorithm consists of two stages:

First stage

Bringing the cost matrix and calculating a lower figure of the toll of the road r.

1. Calculate the smallest element in each row (cast constant for the row)
2. Go to the new cost matrix by subtracting its throw away constant from all row
3. Calculate the smallest element in from each one column (cast constant for the column)
4. Attend the new cost matrix Subtracting from each column its constant of reduction.
Atomic number 3 a result, we have a cost intercellular substance in which in each run-in and in to each one pillar there is at the least matchless zero element.
5. We calculate the boundary at this stage As the add of the reduction constants for the columns and rows (this boundary will be the value to a lesser extent than which it is impossible to construct the desired itinerary)

The secondly (briny) stage

1. Calculation of the penalty for not-employment for each zero chemical element of the slashed cost matrix.
The penalty for not using an factor with index (h, k) in the ground substance means that this edge in is not included in our route, which means that the minimum cost of non using this edge is the sum of the minimum elements in row h and column k.

a) We are sounding for all cardinal elements in the acknowledged matrix
b) For each of them we consider its penalty for not-use.
c) Choose an element that corresponds to the maximum penalty (some, if in that location are several)

2. Now we divide our set S into sets containing the boundary with the uttermost penalty (S _w ) and not containing this edge (S _{w / o} ).
3. The computing of cost estimates for routes enclosed in each of these sets.
a) For the set S _{w / o,} everything is two-needled: since we do not bring out the corresponding edge with the maximum penalty (h, k), then for it the be estimate is capable the cost estimate of the set S + punishment for not using the edge (h, k)
b) When calculative of costs for the placed S _w, we take into account that since the edge (h, k) enters the road, then the edge (k, h) cannot enter the road, therefore we write c (k, h) = infinity in the cost matrix, and since we sustain already "left" charge h and "already arrived" at point k, then no margin coming out of h, and non one edge coming in k can be used, therefore we blue-pencil from monetary value matrices row h and column k. After that, we present the matrix, and so the be appraisal for S _wadequate the sum of the cost estimates for S and r (h, k), where r (h, k) is the sum of the reduction constants for the changed cost matrix.
4. Of each the non-broken sets, matchless that has the smallest reckon is chosen.

So we continue until in the matrix of expenses there is not one crossed outer words and one not crossed out column.

Small optimization - get in touch heuristics

Yes, literal, why don't we inaugurate heuristics? Indeed, in the algorithmic program of branches and borders, we actually bod a tree at whose nodes we decide to film an butt (h, k) operating theatre not, and hang deuce children - Sw (h, k) and Sw / o (h, k). Only the best choice for the incoming iteration is designated only by assessment. So let's prefer the best non only by assessment, but too by depth in the tree, because the deeper the selected item, the closer IT is to the terminate of the count. Thence, we rump finally wait for an respond.

Now, actually, about the errors in this issue

There was single one mistake - one should choose a set with a minimum boundary from among all realizable paths for splitting, and not from two children resulting from the stopping point splitting.

Evidence

Lashkar-e-Taiba's go back to the video at the beginning of the post:

And here is the solution with the corrected algorithm:

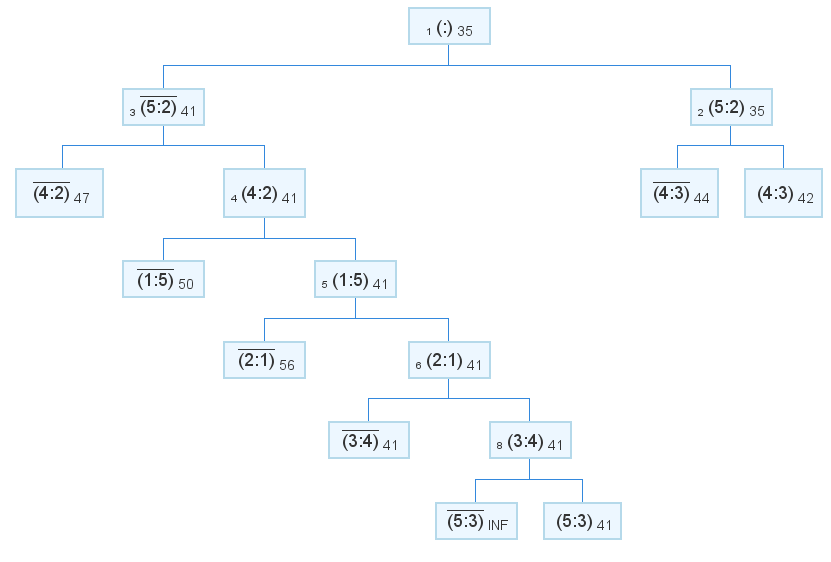
Answer: itinerary: 3 => 4 => 2 => 1 => 5 => 3 length: 41
Atomic number 3 you can see, including the 5: 2 boundary in the answer will embody an error. As necessary, the

graph Comparison of the branches and borders method acting and the time spent for a random tabular array from 5x5 to 10x10: The

graph of the maximum and marginal meter dog-tired for matrices from 5x5 to 66x66.

You can try out with a detailed answer here .
measurement information were obtained from 100 random matrices. not too good a number, but a general idea provides.
Sources on GitHub (updated).

DOWNLOAD HERE

GET Solving the traveling salesman problem using the branch and bound method / Sudo Null IT News FREE

Posted by: burrowswituabled.blogspot.com

Share this post